|  |  |
Metodo del valore a rischio
Posto m come multiplo della deviazione standard che determina l'intervallo di confidenza della stima, si definisce livello di sicurezza la probabilità di ottenere perdite non eccedenti il VAR.
Per ridurre la probabilità di ottenere perdite superiori al VAR stimato, e quindi alla dotazione patrimoniale fissata in corrispondenza, occorre aumentare il multiplo m, sino ad ottenere un intervallo di confidenza dell’ampiezza desiderata. Assumendo, come nei procedimenti di stima della volatilità 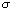 , distribuzioni normali dei fattori con media nulla, i calcoli relativi sono molto semplici. Il rapporto tra lo shock x e la volatilità si distribuisce, essendo nulla la media, secondo una normale standardizzata. La probabilità di ottenere shock non superiori, in valore assoluto, a una soglia xe è pari a: , distribuzioni normali dei fattori con media nulla, i calcoli relativi sono molto semplici. Il rapporto tra lo shock x e la volatilità si distribuisce, essendo nulla la media, secondo una normale standardizzata. La probabilità di ottenere shock non superiori, in valore assoluto, a una soglia xe è pari a:
dove 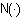 è la funzione di probabilità cumulativa di una variabile casuale distribuita normalmente. Ad esempio, per è la funzione di probabilità cumulativa di una variabile casuale distribuita normalmente. Ad esempio, per 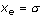 tale probabilità è pari a: tale probabilità è pari a:
Graficamente la probabilità di osservare variazioni comprese nell’intervallo di confidenza corrisponde all’area sottostante la funzione di densità di 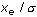 tra –1 e 1. L’area posta sotto le code esprime la probabilità di shock in assoluto superiori al valore soglia. Per tra –1 e 1. L’area posta sotto le code esprime la probabilità di shock in assoluto superiori al valore soglia. Per 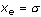 , risulta essere 0,16 + 0,16 = 0,32 (si veda la figura seguente). , risulta essere 0,16 + 0,16 = 0,32 (si veda la figura seguente).
Se m = 1, allora la probabilità di subire perdite superiori al VAR è uguale a quella di shock di entità superiore a 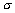 , che però siano anche di segno sfavorevole. Se la posizione è lunga ciò corrisponde alla probabilità di ottenere shock negativi inferiori a - , che però siano anche di segno sfavorevole. Se la posizione è lunga ciò corrisponde alla probabilità di ottenere shock negativi inferiori a -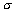 , se è corta alla probabilità di shock positivi superiori a , se è corta alla probabilità di shock positivi superiori a 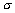 . Grazie alla simmetria della distribuzione normale, la probabilità di superare la soglia è uguale nelle due direzioni (per m = 1 è il 16%, corrispondente a un livello di protezione dell’84%). Ne deriva una stima della perdita potenziale che prescinde dal segno della posizione. Per comodità, la calcoliamo come probabilità di ottenere uno shock inferiore a –xe, giungendo alla seguente relazione tra “livello di sicurezza” (ovvero probabilità di perdite non eccedenti il VAR) e m: . Grazie alla simmetria della distribuzione normale, la probabilità di superare la soglia è uguale nelle due direzioni (per m = 1 è il 16%, corrispondente a un livello di protezione dell’84%). Ne deriva una stima della perdita potenziale che prescinde dal segno della posizione. Per comodità, la calcoliamo come probabilità di ottenere uno shock inferiore a –xe, giungendo alla seguente relazione tra “livello di sicurezza” (ovvero probabilità di perdite non eccedenti il VAR) e m:
Il segno della posizione netta è ininfluente sul VAR a livello di singolo fattore, mentre è importante quando si aggregano i rischi rispetto a diversi fattori poiché determina, a seconda del segno della correlazione, un effetto di compensazione o di accumulo dei rischi. Nella tabella seguente si riporta il valore di m per vari intervalli di confidenza.
Livello di sicurezza (%) | Multiplo della deviazione standard (m) |
99,5 | 2,5 |
97,5 | 2,0 |
95,0 | 1,6 |
90,0 | 1,3 |
84,0 | 1,0 |
Un’istituzione fisserà un livello di protezione crescente in funzione della propria avversione al rischio. Un m più elevato porta a requisiti patrimoniali più onerosi e, conseguentemente, a indici di redditività risk adjusted inferiori. Peraltro a livello tanto di singolo fattore quanto di portafoglio, m è un fattore di scala lineare del VAR, per cui variando m non si modificano i rapporti tra VAR di portafogli diversi.
Fonte [[Erzegovesi97:224-226]]
Categoria: Risk management
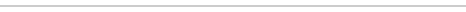
 | |