|  |  |
Breve storia dei principali modelli di valutazione delle opzioni
Valutazione in base a modelli assicurativi
- La moderna teoria dell'option pricing nasce con il modello di Black-Scholes-Merton nei primi anni Settanta. In precedenza la teoria finanziaria aveva affrontato il problema nella cornice della valutazione delle attività rischiose, con estensioni del CAPM . Nella pratica, invece, l'attività di trading in opzioni era vista come un'attività quasi assicurativa: i market maker assumevano posizioni che trovavano naturale compensazione in contratti di segno opposto (ad esempio acquisti contro vendite di call) o in trasformazioni equivalenti (vendite di call contro acquisti di put e vendite a termine). Sulle posizioni non compensate il market maker sosteneva un rischio che veniva coperto dal suo patrimonio. Il premio di equilibrio era determinato alla stregua di un premio assicurativo. Ipotizzando la prevalenza di una domanda di acquisto di opzioni da parte degli utenti finali, i market maker tendevano normalmente a posizionarsi come emittenti netti, e dovevano pertanto fronteggiare un'esposizione aperta sulle opzioni short. Per coprire le conseguenti perdite attese in caso di esercizio era cruciale fissare livelli di premio adeguati. Le quotazioni venivano fissate in base alla distribuzione prevista dei prezzi del sottostante, che è la base per calcolare, dato lo strike, la perdita attesa dell'emittente. Tali distribuzioni, rappresentate in modo più o meno rigoroso, risentivano delle attese soggettive dei trader. Il premio era fissato aggiungendo alla perdita attesa un margine adeguato a coprire i rischi sopportati, che ad evidenza crescevano con l'entità dell'esposizione netta (ammontare e concentrazione su sottostanti e tipi di opzione) e con l'incertezza sui prezzi futuri. In un contesto del genere, i premi delle opzioni erano molto sensibili alla struttura della domanda e alla conseguente pressione sulle posizioni nette dei market maker: un simile modello di economicità non è praticabile con sicurezza.
I modelli di pricing in tempo discreto
- Nella realtà il prezzo tra la data iniziale e la fine di un periodo di tre mesi subisce più di una variazione aleatoria e può raggiungere a scadenza un numero assai elevato, teoricamente infinito, di possibili valori. I modelli nel continuo ipotizzano che il mercato funzioni 24 ore su 24 e che faccia segnare una serie infinita di prezzi con variazioni istantanee su intervalli infinitesimali. Nel modello di Cox, Ross e Rubinstein del 1979 una via intermedia assumendo che sul mercato la domanda e l'offerta si incontrino con frequenza regolare in una successione discreta di istanti e che si formi una serie discreta di prezzi.
Rappresentiamo quindi l'andamento del prezzo nel tempo e negli stati di mercato (nello spazio) dei prezzi tra la data iniziale e la scadenza dell'opzione mediante un reticolo definito per una serie di n momenti futuri, fra loro equidistanti. La distanza temporale tra i nodi è pari all'intervallo 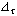 , quindi la durata dell'opzione è pari a n , quindi la durata dell'opzione è pari a n 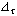 . Il reticolo è costruito come albero binomiale seguendo regole identiche a quelle che determinano la forbice dei prezzi nel caso uniperiodale: in ogni intervallo il prezzo, partendo da un livello iniziale Sk può raggiungere soltanto due stati reciprocamente esclusivi, ovvero può aumentare di un fattore u con probabilità q o diminuire di un fattore d con probabilità 1-q. Per mantenere una descrizione compatta del reticolo, si ipotizza che questi fattori non varino nel tempo e con i prezzi (volatilità costante). . Il reticolo è costruito come albero binomiale seguendo regole identiche a quelle che determinano la forbice dei prezzi nel caso uniperiodale: in ogni intervallo il prezzo, partendo da un livello iniziale Sk può raggiungere soltanto due stati reciprocamente esclusivi, ovvero può aumentare di un fattore u con probabilità q o diminuire di un fattore d con probabilità 1-q. Per mantenere una descrizione compatta del reticolo, si ipotizza che questi fattori non varino nel tempo e con i prezzi (volatilità costante).
Nonostante i limiti che lo caratterizzano, il modello binomiale è un impagabile strumento formativo e di analisi, poiché consente di "fermare l'immagine" su momenti definiti della vita dell'opzione. Per questo motivo i modelli binomiali, con semplici estensioni, possono essere applicati ai casi in cui il valore dell'opzione dipende da eventi che si verificano durante la sua vita e dalle decisioni prese di conseguenza dal detentore. Ad esempio, il modello di CRR è lo standard per il pricing delle opzioni americane grazie alla possibilità di simulare al suo interno la decisione di esercizio anticipato. In molti casi gli alberi binomiali, o loro estensioni, sono strumenti per la costruzione di prototipi di modelli di valutazione che possono essere riformulati nel continuo.
I modelli di pricing nel continuo
- Aumentando il numero di passi di un albero binomiale, si generano distribuzioni separate da intervalli sempre più brevi e con valori di prezzo sempre più numerosi. La probabilità di ottenere un prezzo specifico a una certa data si riduce di conseguenza. Parallelamente diventano più precise le misure delle probabilità cumulative, cioè di ottenere ad una certa data un prezzo superiore o inferiore a un livello soglia. Se ne ricava una rappresentazione della dinamica del mercato tendenzialmente completa. Se noi facciamo tendere a zero la lunghezza degli intervalli
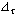 , l’albero binomiale evolve in un processo stocastico nel continuo che non può più essere rappresentato da un numero finito di punti stato/tempo associati a probabilità definite. Il piano spazio-temporale è saturato da un numero infinito di percorsi alternativi del prezzo, e ognuno di questi percorsi è tracciato da una serie infinita di prezzi che si formano ogni istante, modificandosi sotto l’impulso di variazioni infinitesimali, in parte prevedibili e in parte aleatorie. Trasponendo le regole di costruzione di una posizione coperta dal discreto al continuo, si arriva a modelli di pricing sostanzialmente affini a quello binomiale, ma espressi in un linguaggio matematico più conciso e trattabile analiticamente. , l’albero binomiale evolve in un processo stocastico nel continuo che non può più essere rappresentato da un numero finito di punti stato/tempo associati a probabilità definite. Il piano spazio-temporale è saturato da un numero infinito di percorsi alternativi del prezzo, e ognuno di questi percorsi è tracciato da una serie infinita di prezzi che si formano ogni istante, modificandosi sotto l’impulso di variazioni infinitesimali, in parte prevedibili e in parte aleatorie. Trasponendo le regole di costruzione di una posizione coperta dal discreto al continuo, si arriva a modelli di pricing sostanzialmente affini a quello binomiale, ma espressi in un linguaggio matematico più conciso e trattabile analiticamente.
Il modello sviluppato quasi contemporaneamente da Fischer Black e Myron Scholes, e da Robert Merton nel 1973 segna la pietra miliare dei modelli finanziari in tempo continuo, con riflessi che vanno oltre l’ambito dell’option pricing. La formulazione originale riguarda le opzioni europee su azioni scambiate a pronti. Nel 1976 Black proponeva un’estensione alle opzioni su contratti a termine, basata su una formulazione equivalente al modello base e matematicamente più parsimoniosa.
Nel 1983 Garman e Kohlhagen dimostrarono come il modello base di Black-Scholes-Merton, elaborato per la valutazione delle opzioni azionarie, possa essere esteso, con le sue assunzioni di base, alle opzioni valutarie. In particolare, il modello originario non fornisce una corretta valutazione delle opzioni su valute, poiché in queste ultime sono coinvolti due tassi d’interesse. Per cui il modello di Garman-Kohlhagen, che ricalca il modello dei “dividendi proporzionali” di Samuelson e Merton, vede la sua originalità nel fatto di considerare il ruolo chiave dei tassi d’interesse privi di rischio applicati sulle valute coinvolte nel contratto d’opzione. Nello stesso anno in cui Garman e Kohlhagen elaborarono il loro modello un altro autore, Grabbe, pubblicò una sua formula di valutazione delle opzioni valutarie di stile europeo, riprendendo il modello di Black del ’76. L’elemento che contraddistingue questi due modelli consiste nel fatto che mentre il modello di Garman-Kohlhagen utilizza il cambio spot, quello di Grabbe utilizza il cambio a termine. Tuttavia, se viene applicata la teoria keynesiana della parità dei tassi d’interesse, si può agevolmente dimostrare come i due modelli siano in realtà le facce di una stessa medaglia.
In definitiva, l'estensione di Garman e Kohlhagen include i modelli di Black-Scholes-Merton e di Black come casi particolari.
Fonte [[SamuelsonMerton69:17-46]], [[BlackScholes73]], [[Merton73]], [[Black76]], [[CoxRossRubinstein79]], [[GarmanKohlhagen83]], [[Grabbe83]], [[Smithson92]], [[Erzegovesi97]]
Categoria: Strumenti finanziari
 | |